Let's Share it

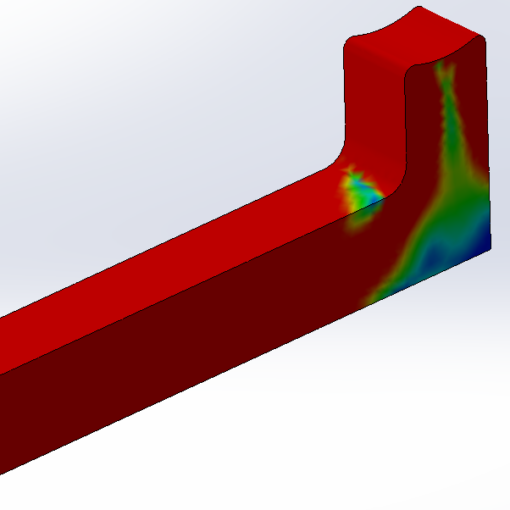
Following the previous whitepaper, in this article we are going to check how much the FEA results are reliable and if the high stress results mean part failure or not. At the beginning, it should be admitted that there isn’t any specific and general answer to this question; however, it is tried to provide some advice for achieving a more accurate judgement.

It is tried to avoid explaining theories and they are just mentioned and refereed to some reliable sources.

At this article we will review:

Reasons of high stress values,
Failure theories
Interpret the Results

Assumption

For the purpose of this article, it is assumed that the model, boundary conditions, contact types, load types and directions, mesh size and quality are correct and are accurate replicators of reality.

Let’s start with stress review and check what are the possible reasons for high stress values.

Reasons of high stress values

In addition to high level of loads, boundary conditions and contacts that could lead to high stress results, analysis type could be another reason of high stress values.

Linear Static analysis, as the name suggests, assumes linear relationship between strain and stress (σ= Eε, Hook’s law), as the part continue to deform (increase strain) the stress is increased accordingly and beyond the yield stress it leads to unrealistic and high stress value, figure (1) [ductile material stress- strain curve].

Stress Strain Curve — Figure (1)- Realistic VS Incorrect Stress Values

Failure Theories

Before continuing this discussion, we need to have a look at the material type, generally we divide materials into two groups of ductile and brittle. The main differences between ductile and brittle materials could be found in the table (1).

Table of comparison table — Table (1)- Ductile VS Brittle Materials

Regarding to the strength of materials, we always have results from unaxial tension test; while in reality, most of the times parts are experiencing all terms of stress (nine terms of stress); then, we need tools to make comparison between reality and the test results possible.

These tools are:

For Ductile Materials (Yield Criteria):

Maximum Shear Stress (Tresca theory),
Distortion Energy (Von-Mises theory),
Ductile Coulomb-Mohr [for ductile materials where the tensile and compressive are not the same scalars].

For Brittle Materials (Fracture Criteria):

Maximum Normal Stress,
Brittle Coulomb-Mohr,
Modified Mohr.

For complete explanation about these theories, please refer to Mechanical Engineering Textbooks like “Shigley’s Mechanical Engineering Design., reference of this section”.

Interpret the results

Stress Check (Von-Mises)

The first thing that we always check is the Von-Mises stress distribution of the model to use a scalar number (Von-Mises Stress here) to part yield stress. If the stress all over the part is below the material yield stress the part could withstand the load. What if the stress is above the yield stress in some areas.

In such cases, before making any decision we need to do some further checks.

Note: for brittle materials in SolidWorks Simulation, you could use Tresca stress.

Comparison with simplified model

Especially for the structural elements, you could compare the behavior of the part/ stress level with available mathematical formula of the same or simplified geometry, so that you have a reference point for comparison, a good resource for calculation for structural elements is AS4100.

Non-Linear Analysis

Especially for mechanical elements due to the geometry complexity most of the times we don’t have the luxury of access to mathematical equations. In this case we need to run non-linear analysis.

For this type of analysis, we need to define material properties accordingly. In here, we got three options, option one is the stress-strain curve of the material, option two is simplified stress-strain curve by defining tangent modulus (Et) to account for material work hardening or assume there is no work hardening (Et=0) and the stress after yield point doesn’t change, Figure (2).

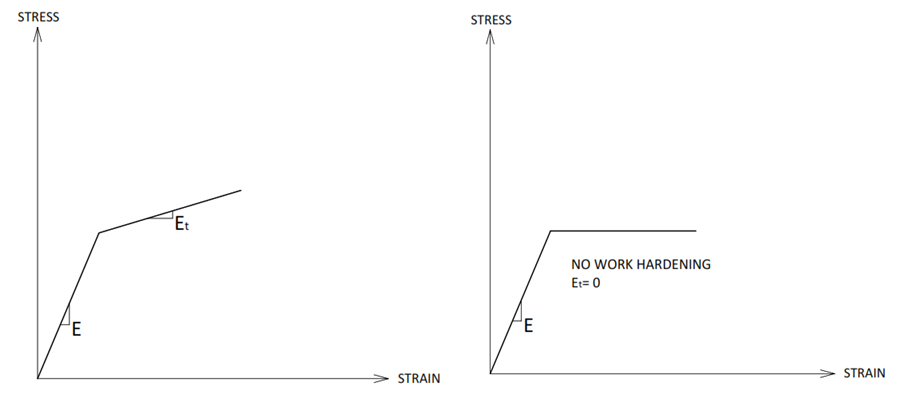
Stress-Strain Curve for material with work hardening on right, without work hardening on left — Figure (2)- Stress- Strain curve for material with work hardening (Right), without work hardening (left)

As it could be understood from the figure(2), using material without work hardening adds a margin of safety to design and you don’t need to be worry if work hardening happens or not for your material.

Having said that, you might design based on a specific specification or code that allow you to consider some acceptable level of strain hardening (work hardening) in your design.

Other

A good practice to investigate the results accuracy is to check the displacement of the model, does the model displaces as it is expected or not and compare it to the standard/ code limits.

Don’t judge based only one run and check the results at least with three different mesh sizes and check the result’s convergence.

If the high stress area is on a stress concentration zone most likely it is acceptable and it only causes local yield.

At the end, FEA is a tool and should be judged based on the field and practical experience and judgment and it is a good practice to ask someone with more experience to review your findings.

What is Next:

On the next whitepaper, we will try to apply our learning in this whitepaper to the study in the Finite Element- Part 08

whitepaper and see how it could be done in SolidWorks Simulation.

Let’s talk about your project